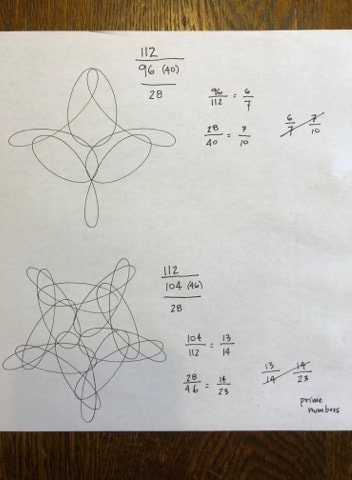
The number of petals (or points, or nodes, or ...) in a design can be predicted by doing a bit of math.
Consider the case of a stationary piece (a ring or gear) and a moving piece (a gear of some sort). They both have a circumference that is expressed by their tooth counts.
Consider the case of a stationary piece (a ring or gear) and a moving piece (a gear of some sort). They both have a circumference that is expressed by their tooth counts.
How to calculate number of points in a design:
Prime Factor Method:
- Write the ratio of the stationary gear over the moving gear; (for example 180/60 for a 60 tooth gear in a 180 ring).
- Replace the numbers with their prime factors; (2*2*3*3*5)/(2*2*3*5)
- Cancel the common factors, numbers that are present on both sides of the fraction. (2*2*3*3*5)/(2*2*3*5)= 3/1
- The top number is the number of petals that the design will have; this is also the number of times the moving piece will rotate.
- The bottom number is the number of times the moving piece will move around the stationary piece.
More math approach:
Two objects, gear-ring or gear-gear work. Take the lowest common factor (LCM) of the tooth count of the two objects. This gives the travel distance, in teeth. Then dividing that number by the tooth count of the moving object; this gives the number of full rotations, and therefor petals, that the design will have.
I specify moving object rather than smaller number because when using one gear around another gear it can be the bigger one that is moving.
Two objects, gear-ring or gear-gear work. Take the lowest common factor (LCM) of the tooth count of the two objects. This gives the travel distance, in teeth. Then dividing that number by the tooth count of the moving object; this gives the number of full rotations, and therefor petals, that the design will have.
I specify moving object rather than smaller number because when using one gear around another gear it can be the bigger one that is moving.
3 Gear Systems:
There is also work being done on making consistent prediction on 3 object systems (a gear in a gear in a ring for example) but the efforts on those so far are proving somewhat inconsistent. This is probably due to there being several ways to count the number of petals or nodes in multi gear systems.
Some metrics have emerged though. This one for finding interesting simple asymmetric designs for example:
"... here’s a fun discovery I made. In a gear in gear in gear system if you have the same number in both the numerator and denominator of the simplified fractions you will get a spiro that has only one direction of symmetry. Even more interesting I found a combination where this is the case but, both the remaining numbers are prime and the spiro has no symmetry at all. Cool huh.
...If the denominator of the ratio between the two large gears is cancelled out by the numerator of the ratio between the two smaller gears you get a butterfly with one line of symmetry. If the numerator is the one that’s cancelled then you get a simple figure with either 2 or 4 lines of symmetry. Whew. Hope that makes sense."
-Julie Schaer
Some metrics have emerged though. This one for finding interesting simple asymmetric designs for example:
"... here’s a fun discovery I made. In a gear in gear in gear system if you have the same number in both the numerator and denominator of the simplified fractions you will get a spiro that has only one direction of symmetry. Even more interesting I found a combination where this is the case but, both the remaining numbers are prime and the spiro has no symmetry at all. Cool huh.
...If the denominator of the ratio between the two large gears is cancelled out by the numerator of the ratio between the two smaller gears you get a butterfly with one line of symmetry. If the numerator is the one that’s cancelled then you get a simple figure with either 2 or 4 lines of symmetry. Whew. Hope that makes sense."
-Julie Schaer
(Almost) Working Hypothosis for Mulit Gear Prediction Math;
beware here there by math dragons and probably some bits that are full on wrong.
To make this description easier I am going to make up a fake example with easy numbers.
Piece A: a 240 tooth ring
Piece B: a 80 tooth gear with a 20 tooth ring cut into it
Piece C: a 12 tooth gear in the 20 tooth ring
we can consider the two simple systems of B in A and C in B. For B in A it is a 3 lobed triangle design; lets call this number N. For C in B it is a 5 lobed design. But because the 20 ring in B is not stationary we must remember that it travels too and so it completes 3 rotations: LCM(12,20)/20=60/20=3; lets call this number M. (This example suffers from both N and M being 3 which I acknowledge is confusing/convenient)
To have a closed design in this system all elements must end up back at their starting point. We know two numbers (N and M) that tell us how many revolutions of B must be completed. In this case because N and M are both 3 this would make a simple design that was closed with 3 'major lobes' and 5 'minor lobes'. For a configuration where N =4 and M=5 then LCM(N,M)=20
I have tried to work this out on some paper and with some though but haven't had a chance to field test it yet so I might be way off. Any confirmation or input would be great. I also know that I've probably glossed over or made some big leaps in my description so let me know if you want more words on any specific part or general confusion. I opted for concise and possibly confusing because I didn't think making it longer would remove the 'possibly confusing' attribute.
Additional excitement: I think that this will make it easier for me to find multi gear systems that yield weird results. There are two sorts of designs that I've seen: the more common braided design where the major lobes from the bigger A-B system interaction is obvious and the minor lobes from the B-C design make a braided mesh that follows that shape, and then the much more elusive designs where they just make an odd loose loops with fewer axis of symmetry and mirror planes and look completely different. I really like these later types but can't consistently make them. I suspect that it has to do with finding systems with N-M values that have common factors so that the LCM(N,M) is quite small.
There is a much more detailed set of articles about Wild Gears math written by Alyx Brett on their blog:
You can find details and discussion about different kinds of symmetry in 3 gear systems on this r/spirograph post by u/HomegrownTomato. It looks at how to predict some fun low density designs and some really stunning sub types of designs like 'butterflies'.
The Wild Gears enthusiast Glagolj has also written deeply about the math and gear selection for multi-gear systems. In addition to their several posts they have also made a web-tool for rendering the output of different gear combinations; it is lovely.
You can find details and discussion about different kinds of symmetry in 3 gear systems on this r/spirograph post by u/HomegrownTomato. It looks at how to predict some fun low density designs and some really stunning sub types of designs like 'butterflies'.
The Wild Gears enthusiast Glagolj has also written deeply about the math and gear selection for multi-gear systems. In addition to their several posts they have also made a web-tool for rendering the output of different gear combinations; it is lovely.